Question 1.170

Let \({\bf v} = 3 {\bf i} \,{+}\, 4 {\bf j} \,{+}\, 5 {\bf k}\) and \({\bf w} = {\bf i} - {\bf j} + {\bf k}\). Compute \({\bf v} + {\bf w}, 3 {\bf v}, 6 {\bf v} + 8 {\bf w}, -2 {\bf v}, {\bf v \,{\cdot}\, w}, {\bf v} \times {\bf w}\). Interpret each operation geometrically by graphing the vectors.

Question 1.171

Repeat Exercise 1 with \({\bf v} = 2 {\bf j} + {\bf k}\) and \({\bf w} = - {\bf i} - {\bf k}\).

Question 1.172

• (a) Find the equation of the line through \((-1,2,-1)\) in the direction of \({\bf j}\).
• (b) Find the equation of the line passing through \((0,2,-1)\) and \((-3,1,0)\).
• (c) Find the equation for the plane perpendicular to the vector \((-2,1,2)\) and passing through the point \((-1,1,3)\).

Question 1.173

• (a) Find the equation of the line through \((0,1,0)\) in the direction of \(3 {\bf i} + {\bf k}\).
• (b) Find the equation of the line passing through \((0,1,1)\) and \((0,1,0)\).
• (c) Find an equation for the plane perpendicular to the vector \((-1,1,-1)\) and passing through the point \((1,1,1)\).

Question 1.174

Find an equation for the plane containing the points (2, 1, \(-1\)), (3, 0, 2), and (4, \(-3\), 1).

Question 1.175

Find an equation for a line that is parallel to the plane \(2x-3y+5z-10=0\) and passes through the point (\(-1\), 7, 4). (There are lots of them.)

Question 1.176

Compute \({\bf v \,{\cdot}\, w}\) for the following sets of vectors:

• (a) \({\bf v} = - {\bf i} + {\bf j}; {\bf w} = {\bf k}\)
• (b) \({\bf v} = {\bf i}+ 2 {\bf j} - {\bf k} ; {\bf w} = 3 {\bf i} + {\bf j}\)
• (c) \({\bf v} = - 2 {\bf i} - {\bf j} + {\bf k}; {\bf w} = 3 {\bf i} + 2 {\bf j} - 2 {\bf k}\)

Question 1.177

Compute \({\bf v} \times {\bf w}\) for the vectors in Exercise 7. [Only part (b) is solved in the Study Guide.]

Question 1.178

Find the cosine of the angle between the vectors in Exercise 7. [Only part (b) is solved in the Study Guide.]

Question 1.179

Find the area of the parallelogram spanned by the vectors in Exercise 7. [Only part (b) is solved in the Study Guide.]

Question 1.180

Use vector notation to describe the triangle in space whose vertices are the origin and the endpoints of vectors a and b.

Question 1.181

Show that three vectors \({\bf a, b, c}\) lie in the same plane through the origin if and only if there are three scalars \(\alpha , \beta, \gamma\), not all zero, such that \(\alpha {\bf a} + \beta {\bf b} + \gamma {\bf c} ={\bf 0}\).

Question 1.182

For real numbers \(a_1, a_2 ,a_3, b_1, b_2, b_3\), show that \[ (a_1 b_1 + a_2 b_2 + a_3 b_3)^2 \le (a_1^2 +a_2^2 + a_3^2) (b_1^2 + b_2^2 + b_3^2). \]

Question 1.183

Let \({\bf u,v,w}\) be unit vectors that are orthogonal to each other. If \({\bf a}= \alpha {\bf u} + \beta {\bf v} + \gamma {\bf w}\), show that \[ \alpha = {\bf a \,{\cdot}\, u}, \beta = {\bf a \,{\cdot}\, v}, \gamma= {\bf a \,{\cdot}\, w}. \] Interpret the results geometrically.

Question 1.184

Find the products \(AB\) and \(BA\) where \[ A=\left[ \begin{array}{c@{\quad}c@{\quad}c} 1 & 5 & 2 \\ 0 & 2 & 3 \\ 1 & 0 & 2 \\ \end{array} \right] \quad \quad \quad B=\left[ \begin{array}{c@{\quad}c@{\quad}c} 2 & 0 & 1 \\ 1 & 3 & 0 \\ 2 & 4 & 1 \\ \end{array} \right]\!. \]

Question 1.185

Find the products \(AB\) and \(BA\) where \[ A=\left[ \begin{array}{c@{\quad}c@{\quad}c} 2 & 1 & 2 \\ 4 & 0 & 1 \\ 1 & 3 & 0 \\ \end{array} \right] \quad \quad \quad B=\left[ \begin{array}{c@{\quad}c@{\quad}c} 3 & 0 & 5 \\ 1 & 2 & 1 \\ 0 & 3 & 1 \\ \end{array} \right]\!. \]

Question 1.186

Let \({\bf a,b}\) be two vectors in the plane, \({\bf a}=(a_1,a_2), {\bf b} = (b_1, b_2)\), and let \(\lambda\) be a real number. Show that the area of the parallelogram determined by a and \({\bf b} + \lambda {\bf a}\) is the same as that determined by a and b. Sketch. Relate this result to a known property of determinants.

Question 1.187

Find the volume of the parallelepiped determined by the vertices \((0,1,0),(1,1,1),\) \((0,2,0),\) \((3,1,2)\).

Question 1.188

Given nonzero vectors a and b in \({\mathbb R}^3\), show that the vector \({\bf v} = \|{\bf a} \| {\bf b} + \|{\bf b} \| {\bf a}\) bisects the angle between a and b.

Question 1.189

Show that the vectors \(\|\textbf{b}\|\textbf{a} +\|\textbf{a}\|\textbf{b}\) and \(\|\textbf{b}\|\textbf{a} -\|\textbf{a}\|\textbf{b}\) are orthogonal.

Question 1.190

Use the triangle inequality to show that \( \| \textbf{v} - \textbf{w} \| \geq \ \Big| \| \textbf{v} \| - \| \textbf{w} \| \Big| \).

Question 1.191

Use vector methods to prove that the distance from the point \((x_1,y_1)\) to the line \(ax+by\) \(=c\) is \[ \frac{|ax_1 + b y_1 -c|}{\sqrt{a^2 + b^2}}. \]

Question 1.192

Verify that the direction of \({\bf b} \times {\bf c}\) is given by the right-hand rule, by choosing \({\bf b}, {\bf c}\) to be two of the vectors \({\bf i,j}\), and \({\bf k}\).

Question 1.193

• (a) Suppose \({\bf a \,{\cdot}\, b} = {\bf a' \,{\cdot}\, b}\) for all \({\bf b}\). Show that \({\bf a} = {\bf a}'\).
• (b) Suppose \({\bf a} \times {\bf b} = {\bf a}' \times {\bf b}\) for all \({\bf b}\). Is it true that \({\bf a} = {\bf a}'\)?

Question 1.194

• (a) Using vector methods, show that the distance between two nonparallel lines \(l_1\) and \(l_2\) is given by \[ d = \frac{|({\bf v}_2 - {\bf v}_1) \,{\cdot}\, ( {\bf a}_1 \times {\bf a}_2)|}{\|{\bf a}_1 \times {\bf a}_2 \|}, \] where \({\bf v}_1, {\bf v}_2\) are any two points on \(l_1\) and \(l_2\), respectively, and \({\bf a}_1\) and \({\bf a}_2\) are the directions of \(l_1\) and \(l_2\). [HINT: Consider the plane through \(l_2\) that is parallel to \(l_1\). Show that the vector \( ({\bf a}_1 \times {\bf a}_2) / \|{\bf a}_1 \times {\bf a}_2\|\) is a unit normal for this plane; now project \({\bf v}_2 - {\bf v}_1\) onto this normal direction.]
• (b) Find the distance between the line \(l_1\) determined by the points \((-1,-1,1)\) and \((0, 0,0)\) and the line \(l_2\) determined by the points \((0,-2,0)\) and \((2,0,5)\).

Question 1.195

Show that two planes given by the equations \(Ax + By + Cz + D_1=0 \) and \(Ax + By + Cz + D_2 =0\) are parallel, and that the distance between them is \[ \frac{|D_1 - D_2|}{\sqrt{A^2 + B^2 + C^2}}. \]

Question 1.196

• (a) Prove that the area of the triangle in the plane with vertices \((x_1, y_1), (x_2, y_2), (x_3, y_3)\) is the absolute value of \[ \frac{1}{2}\, \Bigg|\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 1 & 1 & 1\\ x_1 & x_2 & x_3 \\ y_1 & y_2 & y_3 \end{array} \Bigg|. \]
• (b) Find the area of the triangle with vertices \((1,2), (0,1),(-1,1)\).

Question 1.197

Convert the following points from Cartesian to cylindrical and spherical coordinates and plot:

• (a) \((0,3,4)\)
• (b) \((-\sqrt{2},1,0)\)
• (c) \((0,0,0)\)
• (d) \((-1,0,1)\)
• (e) \((-2\sqrt{3}, -2,3)\)

Question 1.198

Convert the following points from cylindrical to Cartesian and spherical coordinates and plot:

• (a) \((1, \pi /4, 1)\)
• (b) \((3, \pi /6, -4)\)
• (c) \((0, \pi /4, 1)\)
• (d) \((2, -\pi /2, 1)\)
• (e) \((-2, -\pi /2, 1)\)

Question 1.199

Convert the following points from spherical to Cartesian and cylindrical coordinates and plot:

• (a) \((1,\pi/2,\pi)\)
• (b) \((2,-\pi/2,\pi/6)\)
• (c) \((0,\pi/8,\pi/35)\)
• (d) \((2,-\pi/2,-\pi)\)
• (e) \((-1,\pi,\pi/6)\)

Question 1.200

Rewrite the equation \(z= x^2 - y^2\) using cylindrical and spherical coordinates.

Question 1.201

Using spherical coordinates, show that \[ \phi = \cos^{-1} \Big( \frac{{\bf u \,{\cdot}\, k}}{\|{\bf u}\|} \Big), \] where \({\bf u} = x {\bf i} + y {\bf j} + z {\bf k}\). Interpret geometrically.

Question 1.202

Verify the Cauchy–Schwarz and triangle inequalities for \[ {\bf x} = (3,2,1,0) \hbox{and} {\bf y} = (1,1,1,2). \]

Question 1.203

Multiply the matrices \[ A = \Bigg[ \begin{array} &3 & 0 & 1 \\ 2 & 0 & 1 \\ 1 & 0 & 1 \end{array} \Bigg] \qquad \hbox{and } \qquad B = \Bigg[ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} 1 & 0 & 1\\ 1 & 1 & 1\\ 0 & 0 & 1 \end{array} \Bigg]. \] Does \(AB =BA\)?

Question 1.204

• (a) Show that for two \(n \times n\) matrices \(A\) and \(B\), and \({\bf x} \in {\mathbb R}^n\), \[ (AB) {\bf x} = A (B {\bf x}). \]
• (b) What does the equality in part (a) imply about the relationship between the composition of the mappings \({\bf x} \mapsto B {\bf x}, {\bf y} \mapsto A {\bf y}\), and matrix multiplication?

Question 1.205

Find the volume of the parallelepiped spanned by the vectors \[ (1,0,1), (1,1,1), \hbox{and} (-3,2,0). \]

Question 1.206

(For students with some knowledge of linear algebra.) Verify that a linear mapping \(T\) of \({\mathbb R}^n\) to \({\mathbb R}^n\) is determined by an \(n \times n\) matrix.

Question 1.207

Find an equation for the plane that contains \((3,-1,2)\) and the line with equation \({\bf v} =(2,-1,0) + t(2,3,0)\).

Question 1.208

The work \(W\) done in moving an object from (0, 0) to (7, 2) subject to a constant force \({\bf F}\) is \(W = {\bf F \,{\cdot}\, r}\), where \({\bf r}\) is the vector with its head at (7, 2) and tail at (0, 0). The units are feet and pounds.

• (a) Suppose the force \({\bf F} = 10\, \cos\, \theta {\bf i} + 10\, \sin \,\theta {\bf j}\). Find \(W\) in terms of \(\theta\).
• (b) Suppose the force \({\bf F}\) has magnitude of 6 lb and makes an angle of \(\pi /6\) rad with the horizontal, pointing right. Find \(W\) in foot-pounds.

Question 1.209

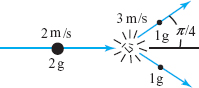
If a particle with mass \(m\) moves with velocity \({\bf v}\), its momentum is \({\bf p} = m { \bf v}\). In a game of marbles, a marble with mass 2 grams (g) is shot with velocity 2 meters per second (m /s), hits two marbles with mass 1 g each, and comes to a dead halt. One of the marbles flies off with a velocity of 3 m/s at an angle of \(45^\circ\) to the incident direction of the larger marble, as in Figure 1.R.1. Assuming that the total momentum before and after the collision is the same (according to the law of conservation of momentum), at what angle and speed does the second marble move?

Figure 1.98: Momentum and marbles.

Question 1.210

Show that for all \(x,y,z\), \[ \Bigg|\begin{array}{@{}c@{\quad}c@{\quad}c@{}} x+2 & y & z \\ z & y+1 & 10 \\ 5 & 5 & 2 \end{array} \Bigg| = - \Bigg| \begin{array}{@{}c@{\quad}c@{\quad}c@{}} y & x+2 & z \\ 1 & z-x-2 & 10-z \\ 5 & 5 & 2 \end{array} \Bigg| . \]

Question 1.211

Show that \[ \Bigg| \begin{array}{@{}c@{\quad}c@{\quad}c@{}} 1 & x & x^2 \\ 1 & y & y^2 \\ 1 & z & z^2 \end{array} \Bigg| \ne 0 \] if \(x,y\), and \(z\) are all different.

Question 1.212

Show that \[ \Bigg| \begin{array}{@{}r@{\quad}c@{\quad}r@{}} 66 & 628 & 246 \\ 88 & 435 & 24 \\ 2 & -1 & 1 \end{array} \Bigg| = \Bigg| \begin{array}{@{}r@{\quad}c@{\quad}r@{}} 68 & 627 & 247 \\ 86 & 436 & 23 \\ 2 & -1 & 1 \end{array} \Bigg|. \]

Question 1.213

Show that \[ \Bigg| \begin{array}{@{}c@{\qquad}c@{\qquad}c@{}} n & n+1 & n+2 \\ n+3 & n+4 & n+5 \\ n+6 & n+ 7 & n+8 \end{array} \Bigg| \] has the same value no matter what \(n\) is. What is this value?

Question 1.214

Are the following quantities vectors or scalars?

• (a) The current population of Santa Cruz, California
• (b) The torque a cyclist exerts on her bicycle
• (c) The velocity of wind blowing through a weather vane
• (d) The temperature of a pizza in an oven

Question 1.215

Find a \(4 \times 4\) matrix \(C\) such that for every \(4 \times 4\) matrix \(A\) we have \(CA=3A\).

Question 1.216

Let \[ A=\left[ \begin{array}{c@{\quad}c} 1 & 1 \\ 0 & 1 \\ \end{array} \right] \quad \quad \quad B=\left[ \begin{array}{c@{\quad}c} 1 & 0 \\ 2 & 1 \\ \end{array} \right] \]

• (a) Find \(A^{-1}, B^{-1}\), and \((AB)^{-1}\).
• (b) Show that \((AB)^{-1} \neq A^{-1}B^{-1}\) but \((AB)^{-1} = B^{-1}A^{-1}\)

Question 1.217

Suppose \(\left[ \begin{array}{c@{\quad}c} a & b \\ c & d \\ \end{array} \right]\) is invertible and has integer entries.

What conditions must be satisfied for \(A=\left[ \begin{array}{c@{\quad}c} a & b \\ c & d \\ \end{array} \right]^{-1}\) to have integer entries?

Question 1.218

The volume of a tetrahedron with concurrent edges a, b, c is given by \(V = \frac{1}{6} {\bf a} \,{\cdot}\, ( {\bf b} \times {\bf c}).\)

• (a) Express the volume as a determinant.
• (b) Evaluate \(V\) when \({\bf a} = {\bf i} + {\bf j} + {\bf k}, {\bf b} = {\bf i} - {\bf j}+ {\bf k}, {\bf c} = {\bf i} + {\bf j}\).

Question 1.219

A tetrahedron sits in \(xyz\) coordinates with one vertex at \((0,0,0)\), and the three edges concurrent at \((0, 0, 0)\) are coincident with the vectors a, b, c.

• (a) Draw a figure and label the heads of the vectors \({\bf a,b,c}\).
• (b) Find the center of mass of each of the four triangular faces of the tetrahedron if a unit mass is placed at each vertex.

Question 1.220

Show that for any vector \({\bf r}\), the center of mass of a system satisfies \[ \sum_{i=1}^n \,m_i \|{\bf r} - {\bf r}_i\|^2 = \sum_{i=1}^n \,m_i \|{\bf r}_i - {\bf c}\|^2 + m \|{\bf r} - {\bf c} \|^2, \] where \(m = {\sum}_{i=1}^n \,m_i\) is the total mass of the system.

Question 1.221

Parallel to the line \(x=3t +1 , y=16t-2, z =- (t+2)\)

Question 1.222

Orthogonal to the plane \(x-6y +z =12\)

Question 1.223

Parallel to both the planes \(8x + y + z =1\) and \(x-y -z =0\)

Question 1.224

Orthogonal to \({\bf i} + 2 {\bf j} - {\bf k}\) and to k

Question 1.225

Orthogonal to the line \(x = 2t-1, y=-t-1, z=t+2\), and the vector \({\bf i}- {\bf j}\)

Question 1.226

At an angle of \(30^\circ\) to i and making equal angles with j and k